

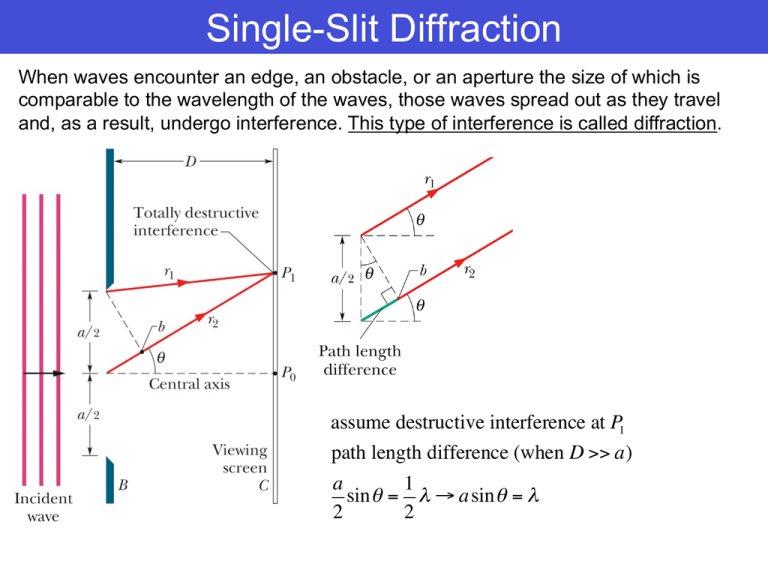
Two rays, each from slightly above those two, will also add constructively. One ray travels a distance λ λ different from the ray from the bottom and arrives in phase, interfering constructively. The difference in path length for rays from either side of the slit is seen to be D sin θ D sin θ.Īt the larger angle shown in Figure 27.22(c), the path lengths differ by 3λ / 2 3λ / 2 for rays from the top and bottom of the slit. There will be another minimum at the same angle to the right of the incident direction of the light.įigure 27.22 Light passing through a single slit is diffracted in all directions and may interfere constructively or destructively, depending on the angle. In fact, each ray from the slit will have another to interfere destructively, and a minimum in intensity will occur at this angle. A ray from slightly above the center and one from slightly above the bottom will also cancel one another.
Thus a ray from the center travels a distance λ / 2 λ / 2 farther than the one on the left, arrives out of phase, and interferes destructively. In Figure 27.22(b), the ray from the bottom travels a distance of one wavelength λ λ farther than the ray from the top. However, when rays travel at an angle θ θ relative to the original direction of the beam, each travels a different distance to a common location, and they can arrive in or out of phase. When they travel straight ahead, as in Figure 27.22(a), they remain in phase, and a central maximum is obtained. (Each ray is perpendicular to the wavefront of a wavelet.) Assuming the screen is very far away compared with the size of the slit, rays heading toward a common destination are nearly parallel. These are like rays that start out in phase and head in all directions. According to Huygens’s principle, every part of the wavefront in the slit emits wavelets.
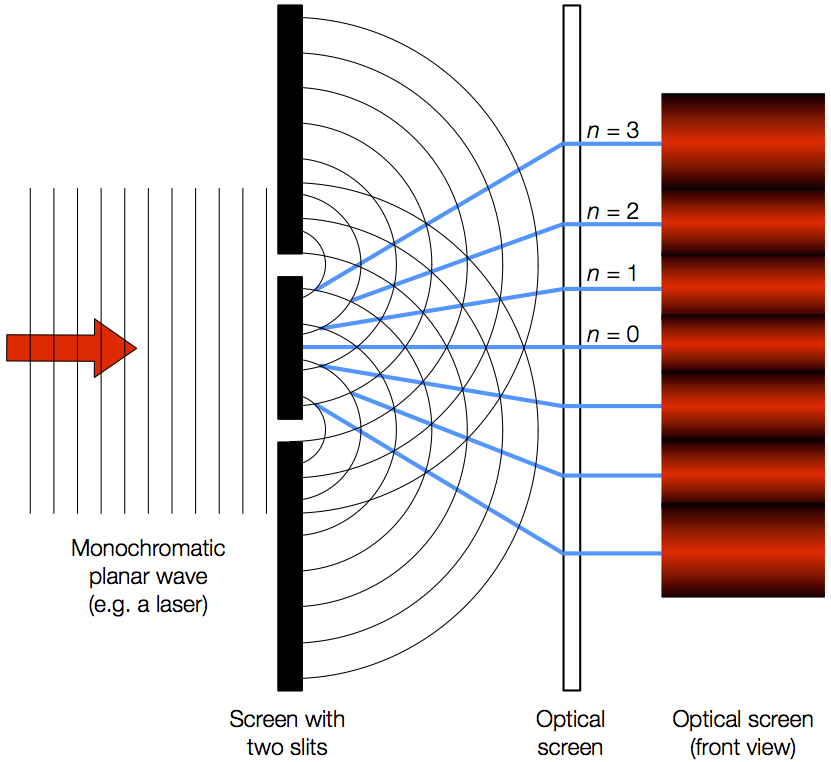
Here we consider light coming from different parts of the same slit. The analysis of single slit diffraction is illustrated in Figure 27.22. (b) The drawing shows the bright central maximum and dimmer and thinner maxima on either side. The central maximum is six times higher than shown. Monochromatic light passing through a single slit has a central maximum and many smaller and dimmer maxima on either side. If the geometry is such that the small angle approximation is valid, the width of the pattern is inversely proportional to the slit width.Figure 27.21 (a) Single slit diffraction pattern. The sketches of the slit widths at right were scaled to the difference between the first minima of the diffraction patterns.

These single slit diffraction patterns were photographed with a helium-neon laser as the light source and a micrometer-controlled single slit. Single Slit Diffraction for Different Slit Widths Note: To obtain the expression for the displacement y above, the small angle approximation was used. The pattern below was made with a green laser pointer. The diffraction pattern at the right is taken with a helium-neon laser and a narrow single slit. If the conditions for Fraunhofer diffraction are not met, it is necessary to use the Fresnel diffraction approach. But an additional requirement is D> a 2/λ which arises from the Rayleigh criterion as applied to a single slit. Fraunhofer Diffraction Fraunhofer Diffraction GeometryĪlthough the formal Fraunhofer diffraction requirement is that of an infinite screen distance, usually reasonable diffraction results are obtained if the screen distance D > a.


 0 kommentar(er)
0 kommentar(er)
